세그먼트 트리란
특정 구간 내 데이터에 대한 연산(쿼리)을 빠르게 구할 수 있는 트리.
ex) 특정 구간 합,최소값,최대값,평균값 등등
Segment : 부분.분할.나누다.분할하다.
시간복잡도
데이터 변경: O(logN)
연산: O(logN)
데이터 변경할때마다 M번 연산: O((logN +logN)*M) = O(MlogN)
https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
문제
어떤 N개의 수가 주어져 있다.
그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려 한다.
만약에 1,2,3,4,5 라는 수가 있고, 3번째 수를 6으로 바꾸고,
2번째부터 5번째까지 합을 구하라고 한다면 17을 출력하면 되는 것이다.
그리고 그 상태에서 다섯 번째 수를 2로 바꾸고 3번째부터 5번째까지 합을 구하라고 한다면 12가 될 것이다.
위와 같은 문제가 주어졌을때,
누적합을 이용해 푼다면 시간복잡도는 아래와 같습니다.
데이터 변경: O(1)
구간합 연산: O(N)
M번의 데이터 변경 때마다 연산:(O(1+N)*M) = O(N*M)
하지만 세그먼트 트리를 이용한다면, O(MlogN)에 가능합니다.
세그먼트 트리 구조
기본적으로 세그먼트 트리는 이진 트리 구조를 가집니다.

이진 트리구조의 특징은 왼쪽 자식노드는 부모 노드의 2배idx를 가집니다.(오른쪽은 2배idx+1)
만약 배열의 크기가 2의 제곱형태이면 완전 이진트리가 될 수 있습니다.
트리의 높이는 Root Node에서 가장 긴 경로를 뜻 하는데, 해당 그래프는 3입니다.
배열의 길이가 8일때, 8 -> 4 -> 2 -> 1.
즉 높이는 배열의 길이를 2^h 형태의 지수 h입니다. (log8 = log2^3 = 3)
이경우 전체 노드 개수는 2^(h+1) -1 이고,수식화하면
높이 h = logN
배열의 크기 2(h+1)-1 입니다.
2의 제곱 형태가 아니라면 h = [logN] + 1 이므로,
(ex 7이면 log7 = 2.xxxx -> 2+1 = 3 )
세그먼트 트리를 저장할 배열의 크기는 2^(h+1) 형태면 크기는 충분합니다.
세그먼트 트리 구현
1) 생성 및 구성
class SegmentTree{
long tree[]; //각 원소가 담길 트리
int treeSize; // 트리의 크기
public SegmentTree(int arrSize){
// 트리 높이 구하기
int h = (int) Math.ceil(Math.log(arrSize)/ Math.log(2));
// 높이를 이용한 배열 사이즈 구하기
this.treeSize = (int) Math.pow(2,h+1);
// 배열 생성
tree = new long[treeSize];
}
// arr = 원소배열, node = 현재노드, start = 현재구간 배열 시작, start = 현재구간 배열 끝
public long init(long[] arr, int node, int start,int end){
// 배열의 시작과 끝이 같다면 leaf 노드이므로
// 원소 배열 값 그대로 담기
if(start == end){
return tree[node] = arr[start];
}
// leaf 노드가 아니면, 자식노드 합 담기
return tree[node] =
init(arr,node*2,start,(start+ end)/2)
+ init(arr,node*2+1,(start+end)/2+1,end);
}
}생성자는 위에서 수식화한 것을 토대로 세그먼트 트리의 배열 사이즈를 정해줍니다.
(자바의 Math.log는 자연로그이므로, 밑을 2로 나누는 효과를 위해 log(2)로 나누기)
Math.ceil을 쓴 이유는 원소 배열의 길이가 2의 제곱꼴이 아닐때 +1 효과를 내기 위해 올림처리를 함.(h = [logN] + 1)
그다음 init 함수로 원소배열(arr)값을 바탕으로 세그먼트 트리의 각 노드에 맞게 넣어줍니다.
init(원소배열,루프노드, 원소배열 시작idx, 원소배열 끝idx)
즉 init(arr,1,1,arr.length-1)을 하게 되면,
재귀형태로 현재노드는 자식노드들의 합을 담으면서 자식노드들을 구하러 들어갑니다.
위에서 얘기했듯이, 왼쪽 자식노드는 부모의 2배 idx를 가지고 절반만큼 부분배열의 합을 구하는 것이니
아래와 같이 구해집니다.(오른쪽은 2*idx+1, (mid+1)~end)
return tree[node] =
init(arr,node*2,start,(start+ end)/2)
+ init(arr,node*2+1,(start+end)/2+1,end);
재귀의 끝 리프노드에 다다르면 부분배열의 시작과 끝이 같아지고(원소가 1개라는 뜻)
그 원소를 세그먼트 트리의 노드에 담으면 됩니다. 그럼 해당 정보를 가지고 재귀를 타고 올라가면서 루프노드까지 구해집니다.
if(start == end){
return tree[node] = arr[start];
}
2) 데이터 변경
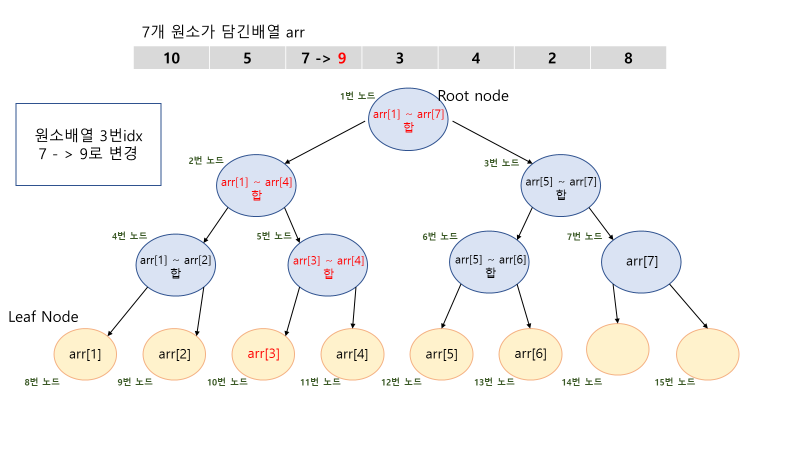
// node: 현재노드 idx, start: 배열의 시작, end:배열의 끝
// idx: 변경된 데이터의 idx, diff: 원래 데이터 값과 변경 데이터값의 차이
public void update(int node, int start, int end, int idx, long diff){
// 만약 변경할 index 값이 범위 바깥이면 확인 불필요
if(idx < start || end < idx) return;
// 차를 저장
tree[node] += diff;
// 리프노드가 아니면 아래 자식들도 확인
if(start != end){
update(node*2, start, (start+end)/2, idx, diff);
update(node*2+1, (start+end)/2+1, end, idx, diff);
}
}데이터 변경 쿼리가 위의 그림같이 들어오면, 원소배열3idx와 관련된 노드들이 다 변경되어야 합니다.
루프노드부터 확인하며 변경된 차이만큼 더해주고, 자식노드들을 확인하러 갑니다.
// 리프노드가 아니면 아래 자식들도 확인
if(start != end){
update(node*2, start, (start+end)/2, idx, diff);
update(node*2+1, (start+end)/2+1, end, idx, diff);
}자식노드의 합 범위가 현재 변경된 idx와 관련이 없으면, 확인을 따로 하지 않습니다.
// 만약 변경할 index 값이 범위 바깥이면 확인 불필요
if(idx < start || end < idx) return;이렇게 체크해가면서 관련된 자식노드들을 다 변경해주면 됩니다.
중요한건 arr 원소배열의 데이터가 변경되어서 segment tree의 노드가 바뀐 것이니,
arr도 데이터 변경을 해놔줘야 추후 같은 위치 idx를 변경할때 정확한 데이터값 차이가 나옵니다.
3) 구간 합 구하기
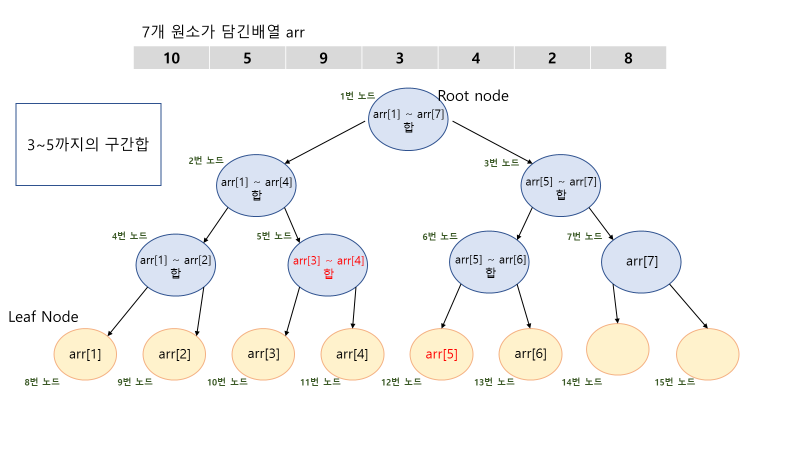
// node: 현재 노드, start : 배열의 시작, end : 배열의 끝
// left: 원하는 누적합의 시작, right: 원하는 누적합의 끝
public long sum(int node, int start, int end, int left, int right){
// 범위를 벗어나게 되는 경우 더할 필요 없음
if(left > end || right < start){
return 0;
}
// 범위 내 완전히 포함 시에는 더 내려가지 않고 바로 리턴
if(left <= start && end <= right){
return tree[node];
}
// 그 외의 경우 좌 / 우측으로 지속 탐색 수행
return sum(node*2, start, (start+end)/2, left, right)+
sum(node*2+1, (start+end)/2+1, end, left, right);
}부분배열의 합을 구하는 쿼리가 들어오면, 루트노드부터 확인합니다.
자식노드로 내려가면서 확인하다가, 현재 배열이 찾고자하는것에 범위에서 벗어나면 0을 반환합니다.
만약 현재 범위가 구하고자 하는 범위내에 완전하게 포함되면, 현재값을 반환합니다.
아니라면 그 밑의 자식을 확인합니다.
최종적으로 다 찾았을때 재귀를 타고 올라오면서 더한값이 반환됩니다.
예제 보기
ex) 3~5까지 구간합 구할때,
1번 루트 노드(1~7) 이므로 자식 확인( return 자식2 + 자식3)
자식2(1~4)안엔 3~4가 해당하므로 자식 확인(return 자식4 + 자식5)
자식4(1~2)는 구하고자하는 3~5에서 벗어나므로 0을 반환
자식5(3~4)는 구하고자하는 3~5에 완전히 포함하므로 값 반환
자식3(5~7)안에 5 해당 (return 자식6 +7)
자식6(5~6)안에 5해당 (return 자식12+13)
자식12(5) 구하고자하는 3~5에 완전 포함 값 반환
기타 나머지 자식들은 다 포함안하므로 0반환
최종 자식5번노드 + 자식12번노드 = 3~5까지의 합이 반환됨
4) 최종 코드
해당 코드는 특정 구간 합을 기준으로 코드가 짜여있지만, 코드를 조금만 수정하면 특정 구간 최소값,최대값 등도 구할 수 있습니다.
static class SegmentTree{
long tree[];
int treeSize;
public SegmentTree(int arrSize){
int h = (int) Math.ceil(Math.log(arrSize)/ Math.log(2));
this.treeSize = (int) Math.pow(2,h+1);
tree = new long[treeSize];
}
public long init(long[] arr, int node, int start,int end){
if(start == end){
return tree[node] = arr[start];
}
return tree[node] =
init(arr,node*2,start,(start+ end)/2)
+ init(arr,node*2+1,(start+end)/2+1,end);
}
public void update(int node, int start, int end, int idx, long diff){
if(idx < start || end < idx) return;
tree[node] += diff;
if(start != end){
update(node*2, start, (start+end)/2, idx, diff);
update(node*2+1, (start+end)/2+1, end, idx, diff);
}
}
public long sum(int node, int start, int end, int left, int right){
if(left > end || right < start){
return 0;
}
if(left <= start && end <= right){
return tree[node];
}
return sum(node*2, start, (start+end)/2, left, right)+
sum(node*2+1, (start+end)/2+1, end, left, right);
}
}
해당 문제 정답코드
https://www.acmicpc.net/problem/2042
/**
* 세그먼트 트리 기본 문제
*
* 세그먼트 트리를 이용하여 데이터 변경 및 구간합 구하기
*
* 배열 구현
*
*/
import java.util.*;
import java.io.*;
public class BJ2042_구간합구하기 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 수의 개수
int m = Integer.parseInt(st.nextToken()); // 데이터 변경 개수
int k = Integer.parseInt(st.nextToken()); // 구간합 구하는 횟수
// 수 저장 배열
long[] arr = new long[n+1];
for(int i = 1; i <= n; i++){
arr[i] = Long.parseLong(br.readLine());
}
SegmentTree stree = new SegmentTree(n);
stree.init(arr,1,1,n);
for(int i = 0; i < m+k; i++){
st = new StringTokenizer(br.readLine());
// 명령어
int cmd = Integer.parseInt(st.nextToken());
int a = Integer.parseInt(st.nextToken());
// 원소의 범위는 2^63이므로 롱타입으로 받아야한다.
long b = Long.parseLong(st.nextToken());
// 데이터 변경 명령어
if(cmd == 1){
stree.update(1,1,n,a,b-arr[a]);
arr[a] = b;
// 구간합 명령어
}else{
bw.write(stree.sum(1,1,n,a,(int)b) +"\n");
}
}
bw.flush();
bw.close();
}
static class SegmentTree{
long tree[];
int treeSize;
public SegmentTree(int arrSize){
int h = (int) Math.ceil(Math.log(arrSize)/ Math.log(2));
this.treeSize = (int) Math.pow(2,h+1);
tree = new long[treeSize];
}
public long init(long[] arr, int node, int start,int end){
if(start == end){
return tree[node] = arr[start];
}
return tree[node] =
init(arr,node*2,start,(start+ end)/2)
+ init(arr,node*2+1,(start+end)/2+1,end);
}
public void update(int node, int start, int end, int idx, long diff){
if(idx < start || end < idx) return;
tree[node] += diff;
if(start != end){
update(node*2, start, (start+end)/2, idx, diff);
update(node*2+1, (start+end)/2+1, end, idx, diff);
}
}
public long sum(int node, int start, int end, int left, int right){
if(left > end || right < start){
return 0;
}
if(left <= start && end <= right){
return tree[node];
}
return sum(node*2, start, (start+end)/2, left, right)+
sum(node*2+1, (start+end)/2+1, end, left, right);
}
}
}
참조
https://hongjw1938.tistory.com/20
자료구조 - 세그먼트 트리(Segment Tree)
1. 세그먼트 트리(Segment Tree, 구간 트리)란? 특정 구간 내 연산(쿼리)에 대해 빠르게 응답하기 위해 만들어진 자료구조이다. 예를 들어 크기가 N=100인 int배열 arr이 있다면 1~100의 인덱스 내 숫자들
hongjw1938.tistory.com
'Algorithm > 개념' 카테고리의 다른 글
| [알고리즘 개념] 소수 구하기, 소수 판별 / JAVA (0) | 2022.01.28 |
|---|---|
| [알고리즘 개념] 펜윅 트리(Fenwick Tree,Binary Indexed Tree) / JAVA (0) | 2022.01.17 |
| [알고리즘 개념] 비트마스크(Bitmask) (0) | 2022.01.14 |
| [알고리즘 개념] KMP - 문자열 검색 알고리즘(JAVA 코드) (0) | 2022.01.12 |
| 정렬 알고리즘(sort) (0) | 2022.01.05 |



댓글