펜윅트리는 세그먼트 트리를 변형한 버전이므로, 세그먼트 트리를 먼저 알아야 이해가 잘 됩니다!
2022.01.17 - [Algorithm/개념] - [알고리즘 개념] 세그먼트 트리(Segment Tree) / Java
그리고 비트 단위로 연산하기 때문에, 비트 연산자를 알아야합니다!
2022.01.14 - [Algorithm/개념] - [알고리즘 개념] 비트마스크(Bitmask)
펜윅트리란(Fenwick Tree, Binary Indexed Tree, BIT)
세그먼트 트리에서 메모리를 절약한 트리.
시간복잡도 O(MlogN)
데이터 변경: O(logN)
연산: O(logN)
공간복잡도 O(N)
펜윅트리는 세그먼트 트리에서 우측 노드를 지운 트리입니다.
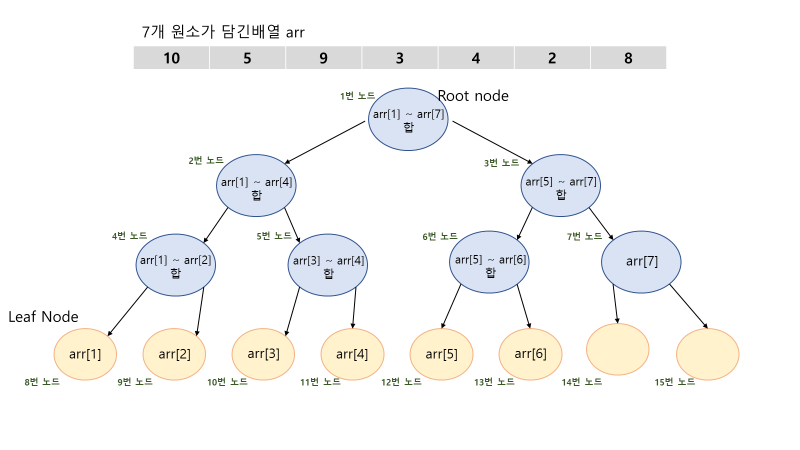

만약 5~7까지의 합을 알고 싶다면, 1~7까지의 합에서 1~4까지의 합을 빼면 알 수 있습니다.
이러한 정보를 토대로 세그먼트 트리상의 우측 노드를 모르더라도 답을 구할 수 있습니다.
즉, 불필요한 정보를 제외한 트리인데, 펜윅트리에선 세그먼트 트리처럼 어떠한 구간의 값을 곧바로 가져올 순 없습니다.
해당 구간의 연산(L~R)을 가져오기 위해선,
R까지의 합(R`)에서 L까지의 합(L`)을 빼고 L을 더하면 구할 수 있습니다.
L~R = R` - L` +L = R` - (L-1)`
세그먼트 트리: getValue(L,R)
펜윅트리 : getValue(R) - getValue(L-1)
펜윅트리 구조

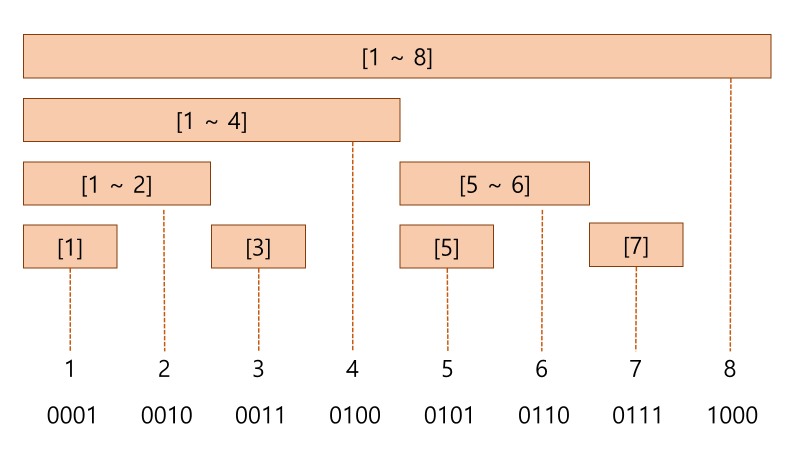
위에서 오른쪽을 지운것을 비트단위로 표현해서 만든 펜윅트리 구조입니다.
펜윅트리에서 노드의 값은 자기자신이거나 자기자신까지의 범위 값일수도 있습니다.
즉, 노드의 idx를 통해서 알 수 있는건 어디부터의 합인지는 모르나, last index는 자신이라는 것을 알 수 있습니다.
펜윅트리 구현
1) 생성
static class FenwickTree{
long tree[];
int treeSize;
public FenwickTree(int arrSize){
tree = new long[arrSize+1];
}
}펜윅트리는 트리의 크기만 지정해주고 관련 정보는 밑에 함수에서 저장할겁니다.
위 그림을 보면, 펜윅트리의 노드는 원소의 개수만큼 생깁니다.
하지만 index로 돌면서 확인할거기때문에, +1 형태로 트리를 생성합니다.
tree = new long[n+1];
2) 데이터 추가 및 변경
public void update(int idx, long diff){
while(idx < tree.length){
tree[idx] += diff;
idx += (idx & -idx);
}
}
위의 함수를 통해서 데이터를 추가하거나 변경할겁니다.
펜윅트리의 구조를 보면, 본인의 바로 상위 노드는 2^n을 더해준 노드라는것을 알 수 있습니다.
이것은 해당 인덱스 비트의 가장 최소 비트를 찾아 더해주면, 상위 노드를 찾아갈 수 있습니다.
예시
예를 들어, 원소 1(0001)의 데이터를 변경하거나 추가하면,
1(0001)에 2^0(0001)을 더해준 index 2(0010)과 관련이 있고,
그 위의 2^1(0010)을 더해준 4(0100) -> 2^2를 더해준 8(1000)의 데이터들이 변경되어야합니다.
idx += (idx & -idx);
의 뜻은 (idx & -idx)를 통해 가장 마지막에 위치한 1의 값을 찾는거고, 그것을 더해 다음 관련노드를 찾아갑니다.
이렇게 최종 배열의 길이를 벗어나기전까지 더해주면서 관련 노드들을 변경해줍니다.
데이터 추가는 처음에 원소 배열의 데이터를 받을때, 펜윅트리에도 데이터를 추가해줍니다.
그럼 관련 노드들을 찾아가면서 다 값을 더해줍니다.
update(노드idx, 해당값);
for(int i = 1; i <= n; i++){
arr[i] = Long.parseLong(br.readLine());
ftree.update(i, arr[i]);
}
3) 특정 구간 연산 구하기
public long sum(int idx){
long result = 0;
while(idx > 0){
result += tree[idx];
idx -= (idx & -idx);
}
return result;
}
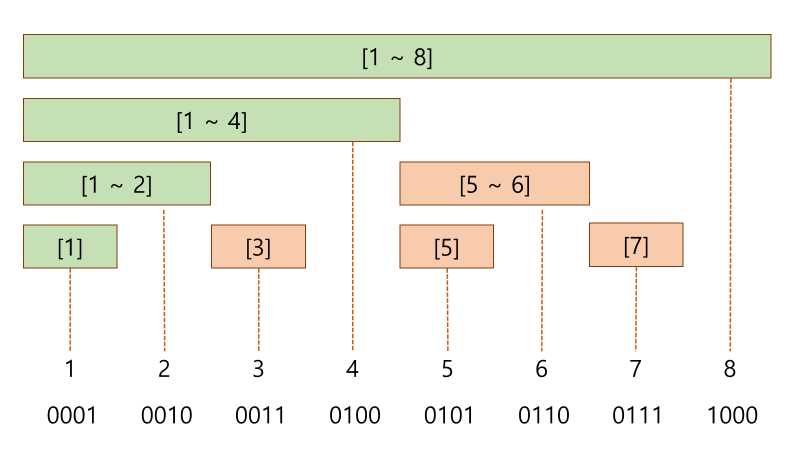
해당 함수(SUM)로 본인 인덱스까지의 합을 구해서 특정 구간 합을 구할 수 있습니다.
(sum(R) - sum(L-1)) = L~R까지의 합
만약 5~7까지의 합을 구한다고하면,
sum(7) - sum(4) 를 통해 구할 수 있는데
sum(7)을 뜯어보면, 7(0111)에서 가장 마지막에 위치한 켜진 비트(1)을 빼가면서 해당 idx의 값을 더해가면 1~7까지의 합을 구할 수 있습니다.
(0111) 7 + (0110)5~6 + (0100)1~4 = 1~7까지의 합
인덱스가 0이되면 종료하면서 다 더한 합을 반환합니다.
4) 전체 코드
static class FenwickTree{
long tree[];
int treeSize;
public FenwickTree(int arrSize){
tree = new long[arrSize+1];
}
public void update(int idx, long diff){
while(idx < tree.length){
tree[idx] += diff;
idx += (idx & -idx);
}
}
public long sum(int idx){
long result = 0;
while(idx > 0){
result += tree[idx];
idx -= (idx & -idx);
}
return result;
}
}
문제를 통한 전체 코드
https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
/**
* 구간합 구하기 펜윅트리 버전 코드
*
*
*/
import java.util.*;
import java.io.*;
public class Test {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 수의 개수
int m = Integer.parseInt(st.nextToken()); // 데이터 변경 개수
int k = Integer.parseInt(st.nextToken()); // 구간합 구하는 횟수
// 수 저장 배열
long[] arr = new long[n+1];
FenwickTree ftree = new FenwickTree(arr.length);
for(int i = 1; i <= n; i++){
arr[i] = Long.parseLong(br.readLine());
ftree.update(i, arr[i]);
}
for(int i = 0; i < m+k; i++){
st = new StringTokenizer(br.readLine());
// 명령어
int cmd = Integer.parseInt(st.nextToken());
int a = Integer.parseInt(st.nextToken());
long b = Long.parseLong(st.nextToken());
// 데이터 변경 명령어
if(cmd == 1){
ftree.update(a,b-arr[a]);
arr[a] = b;
// 구간합 명령어
}else{
bw.write(ftree.sum((int)b) -ftree.sum(a-1) +"\n");
}
}
bw.flush();
bw.close();
}
static class FenwickTree{
long tree[];
int treeSize;
public FenwickTree(int arrSize){
tree = new long[arrSize+1];
}
public void update(int idx, long diff){
while(idx < tree.length){
tree[idx] += diff;
idx += (idx & -idx);
}
}
public long sum(int idx){
long result = 0;
while(idx > 0){
result += tree[idx];
idx -= (idx & -idx);
}
return result;
}
}
}
참조
https://gseok.gitbooks.io/algorithm/content/d2b8-b9ac-c54c-ace0-b9ac-c998/d39c-c705-d2b8-b9ac.html
펜윅 트리 · Algorithm
gseok.gitbooks.io
'Algorithm > 개념' 카테고리의 다른 글
| [알고리즘 개념] 브루트 포스(Brute Force) /Java 코드 (0) | 2022.01.30 |
|---|---|
| [알고리즘 개념] 소수 구하기, 소수 판별 / JAVA (0) | 2022.01.28 |
| [알고리즘 개념] 세그먼트 트리(Segment Tree) / Java (0) | 2022.01.17 |
| [알고리즘 개념] 비트마스크(Bitmask) (0) | 2022.01.14 |
| [알고리즘 개념] KMP - 문자열 검색 알고리즘(JAVA 코드) (0) | 2022.01.12 |


댓글