TreeDP
Tree : cycle이 없는 그래프(서로 다른 두 노드를 잇는 간선이 1개)
TreeDP는 Tree구조에서 서브트리(부분 문제)의 해를 가지고 전체 해를 구하는 방식입니다.
DP에 서브트리의 어떠한 것(서브트리의 노드 개수, 서브트리의 간선 개수 등등)을 저장해둘 것이고,
보통 DFS를 통해 탐색하면서 서브트리의 해를 구해나갑니다.
정점을 기준으로 탐색해나간다면, 보통 O(N)만에 풀립니다.
15681번: 트리와 쿼리
트리의 정점의 수 N과 루트의 번호 R, 쿼리의 수 Q가 주어진다. (2 ≤ N ≤ 105, 1 ≤ R ≤ N, 1 ≤ Q ≤ 105) 이어 N-1줄에 걸쳐, U V의 형태로 트리에 속한 간선의 정보가 주어진다. (1 ≤ U, V ≤ N, U ≠ V)
www.acmicpc.net
/*
1. U를 루트로 하는 서브트리에 속한 정점의 수를 출력
2. tree DP
3. DFS를 통해 서브트리의 노드 개수를 DP에 저장
*/
import java.util.*;
import java.io.*;
public class BJ15681_트리와쿼리 {
public static ArrayList<Integer>[] tree;
public static int[] dp;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 정점의 개수
int r = Integer.parseInt(st.nextToken()); // 루트 정점
int q = Integer.parseInt(st.nextToken()); // 쿼리 개수
dp = new int[n+1];
tree = new ArrayList[n+1];
for(int i = 1; i <= n; i++){
tree[i] = new ArrayList<>();
}
for(int i = 0; i < n-1; i++){
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
tree[a].add(b);
tree[b].add(a);
}
checkSubTree(r); // 정점부터 서브트리 노드 수 파악
for(int i = 0; i < q; i++){
int u = Integer.parseInt(br.readLine());
bw.write(dp[u] +"\n");
}
bw.flush();
bw.close();
}
public static int checkSubTree(int node){
if(dp[node] != 0){ //현재 노드를 방문했었으면 0반환
return 0;
}
dp[node] = 1; // 현재 노드 1개 초기화
for(int next : tree[node]){
dp[node] += checkSubTree(next); // 자식노드의 개수 더하기
}
return dp[node];
}
}
20188번: 등산 마니아
동네 뒷 산에는 등산로가 있다. 등산로는 N개의 작은 오두막들이 N −1개의 오솔길로 이어진 형태이다. 한 오솔길은 두 개의 오두막을 양 방향으로 연결한다. 한 오솔길의 길이는 1이다. 어떤 오
www.acmicpc.net
/**
* 1. 트리 dp문제
*
* 2. 두개의 오두막을 골라 가는 길의 다양성의 총 합을 출력
* 2-1) 예시 1-2-3 이렇게 연결되어 있을때,
* 1-2 1-3 2-3 오두막을 선택할 수 있고,
* 각각의 길의 개수는 1 - 2 - 2 개로 총 5이다.
* 2-2) 내림차순 선택 불가. 2-1
*
* 3. 즉 두개의 오두막을 골라 쓰이는 총 간선의 수를 출력해야한다.
*
* 4. 이걸 간선의 입장으로보면, 각 간선마다 몇번씩 쓰였는지 다 더하면 정답.
*
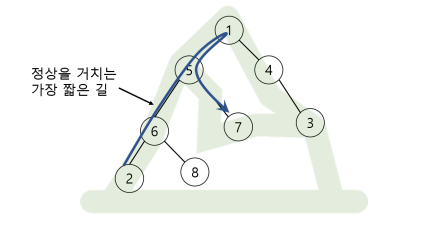
* 5. 예를 들어 2-6으로 이어지는 간선은 2번을 기준으로 위로 이어지는 간선이다.
* 2-6으로 이어지는 간선이 쓰인 개수는,
* 2번을 고르면 나머지 하나는 어떠한 것을 고르든 2-6번은 쓰이게 된다.(정상 오두막을 들려야하므로)
* 그 뜻은 2번을 안고르면 2-6 간선이 안쓰인다는 뜻이므로,
* 전체 고를 수 있는 경우의 수 - 2번을 빼고 고른 경우의 수
* = 2-6번 간선이 쓰인 총 수가 나온다.
* 전체 고를 수 있는 경우의 수는 n(오두막수)C2 = n(n-1)/2
* 2번을 빼고 고른 경우의 수는 n-1C2 = (n-1)(n-2)/2 가 된다.
*
* 하나를 더 봐서, 6-5 간선은
* 6아래의 서브트리(2,6,8) 중에 어떠한 것을 고르든 쓰인다.
* 이 외의 것들중에 2개를 골라야 이 간선이 안쓰이므로,
* 전체 경우의수 - (전체 오두막 수 - 6아래 서브트리)에서 고른 수가 된다.
*
* 루트 정점을 제외한 전체 오두막에서 각 간선별 쓰인 갯수를 다 더하면 정답.
*
* 6. 그럼 이제 서브트리 별 오두막의 수를 구하면 되는데,
* 각 서브트리 별 오두막의 수는 DP에 저장할 것이다.
*
* 7. 각 서브트리 즉, 이어진 오두막은 DFS를 통해 들릴 것이다.
* 최종 끝 오두막은 1개이고,
* 그 위의 오두막들에 그 개수를 더해주면서 최종 정상 오두막까지 구할 것.
* O(N) 풀이
*/
import java.io.*;
import java.util.*;
public class 등산마니아{
static ArrayList<Integer>[] tree;
static int[] dp;
static int n;
static long result = 0;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(br.readLine());
tree = new ArrayList[n+1];
for(int i = 1; i <= n; i++){
tree[i] = new ArrayList<>();
}
dp = new int[n+1];
StringTokenizer st;
for(int i = 0; i < n-1; i++){
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
tree[a].add(b);
tree[b].add(a);
}
dp(1);
}
public static int dp(int now){
dp[now] = 1;
for(int next : tree[now]){
if(dp[next] == 0){
dp[now] += dp(next);
}
}
//정점을 제외한 각 오두막의 위로 이어진 간선이 쓰인 개수 더하기
if(now != 1){
result += comb(n) - comb(n - dp[now]);
}
return dp[now];
}
// N개에서 2개를 고르는 경우의 수
public static long comb(int n){
return (long)n * (long)(n-1)/2;
}
}'Algorithm > 개념' 카테고리의 다른 글
| [알고리즘 개념] 브루트 포스(Brute Force) /Java 코드 (0) | 2022.01.30 |
|---|---|
| [알고리즘 개념] 소수 구하기, 소수 판별 / JAVA (0) | 2022.01.28 |
| [알고리즘 개념] 펜윅 트리(Fenwick Tree,Binary Indexed Tree) / JAVA (0) | 2022.01.17 |
| [알고리즘 개념] 세그먼트 트리(Segment Tree) / Java (0) | 2022.01.17 |
| [알고리즘 개념] 비트마스크(Bitmask) (0) | 2022.01.14 |



댓글